Lambda 整定定律的基本原理
發(fā)布時間:2013-09-18 作者:Vance VanDoren
Lambda整定是一種內(nèi)模控制(IMC)的形式,它能夠使比例積分(PI)控制器在設定點變化時實現(xiàn)平滑、不震蕩的控制效果。它的名字來自于希臘字母 lambda (λ),這是一個用戶較為關心的參數(shù),意味著控制器將過程變量從點A移動到點B需要花費多少時間。
與著名的Ziegler-Nichols整定類似,Lambda整定引入了一組公式或者整定規(guī)則,藉此將PI參數(shù)的值調(diào)整至所需的控制器性能。應用這些公式或者整定規(guī)則的第一步就是確定過程對于控制效果的響應程度和響應速度(見沖擊試驗示意圖)。
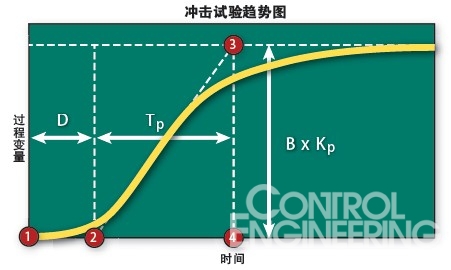
一旦過程的行為能夠用過程參數(shù)(過程增益Kp、過程時間常數(shù)Tp以及死區(qū)時間D)來描述,那么控制器的調(diào)整就比較簡單了。只要將這些值和用戶所選擇的λ帶入“Lambda 整定定律”的公式,就能夠得到PI參數(shù)Kc和Ti的值。
需要指出的是這些調(diào)整規(guī)則僅允許用戶指定一個性能參數(shù):λ。這不僅僅是為了簡化Kc和Ti的計算過程,還是為了讓用戶能夠通過具有物理意義的參數(shù)來選擇控制器的預期性能,而不使用那些沒那么直觀的概念,例如比例帶寬和重置時間。
閉環(huán)性能
從理論上講,如果工作在閉環(huán)模式下,PI控制器整定能夠在4λ的時間內(nèi)完成設定點變更,而且不會出現(xiàn)過調(diào)。這意味著控制器將會使過程變量逐漸地朝向設定點變化,兩者之間的差值會穩(wěn)步地減小。
當過程變量受到嚴格限制,不能超過某些過程限制值的時候,這種過阻尼特性就很有用。控制器永遠不會超出這種限制,因為過程變量不會超過設定值。Lambda整定控制器也不會給過程變量帶來不穩(wěn)定的震蕩,因為在設定點變化之后它無需做反向調(diào)整。過程變量總是會逐漸增加或者是逐漸減小直至達到新的設定點。
過阻尼特性還能夠幫助確保一致性,這也是為什么Lambda整定法在造紙作業(yè)中非常普及的原因,因為某些過程變量的震蕩會給最終產(chǎn)品帶來視覺可見的瑕疵。沒有了過調(diào),執(zhí)行器就不會一下子同時震蕩,造紙機的設備也不會發(fā)生劇烈振動。每一個執(zhí)行器(特別是閥門)的磨損也會更小,因為除非設定點反向調(diào)整,否則它們無需做反向調(diào)整。
多回路協(xié)調(diào)
而且,由于Lambda整定法允許PI控制器在用戶指定的時間間隔內(nèi)達到整定目標,那么它就可以用于將多個回路作業(yè)中的控制器同步,這樣一來過程變量就都會以幾乎同樣的速度變化。這一特性同樣能夠給造紙行業(yè)帶來好處,在混合作業(yè)中它能夠維持配料比率的恒定。
相反地,當某一個相互作用的回路相比于其他回路更加重要,那么可以給這個關鍵回路分配一個較小的λ,以確保它能夠以最小的時間間隔向設定點變化。那些對整體作業(yè)效果貢獻不大的回路以及執(zhí)行器動作較慢或執(zhí)行器沒那么大功效的回路可以指定較大的λ值。
對兩個交互回路使用完全不同的λ值還能夠幫助將兩者去耦,從快回路的角度來看慢回路的整定效果很小或者沒有效果,因為在快回路完成設定點變化的很短的時間內(nèi),慢回路更像靜止不動。相反的,當慢回路開始表現(xiàn)出效果時,快回路已經(jīng)完成任務了。這種去耦是不完全的,但是這兩個回路之間的交互作用在一定程度上會減小,因此兩者之間的負載也會有所減少。
強大的平臺
Lambda整定法還具有一個不那么明顯的優(yōu)點,就是其魯棒性。由于Lambda整定控制器比較保守,它能夠接受一定程度的過程變量預估值和實際值之間的差異,不管這種差異是來自于沖擊試驗的執(zhí)行不當還是由于過程變化發(fā)生于調(diào)整結束之后。計算得到的PI參數(shù)的會因此有些失真,但正是由于這些失真,相比于對過程行為的完全掌控,控制器才能夠獲得一定程度的保守性,但是不管怎樣,閉環(huán)系統(tǒng)還是具有過阻尼特性。
缺點
從另一方面看,Lambda整定法也有其局限性,特別是要求快速調(diào)整時。這種調(diào)整會使過程變化越來越慢,是過程變量和設定值之間長時間保持一個偏離。明確地說,λ的值通常在Tp和3Tp之間,這樣一來對于設定點變化的閉環(huán)響應時間就是相應的開環(huán)階躍響應時間的3倍。而且如果死區(qū)時間D比較長,那么還需要更大的λ值。這種情況下,λ > D就是實際操作中的時間下限,因為控制器不可能比死區(qū)時間響應的更快。
但是Lambda整定控制器的最具有挑戰(zhàn)缺點就是它應對過程外部負載的能力過于有限。雖然當隨機負載使過程變量偏移時Lambda整定法最終還是能夠?qū)⑦^程變量帶回設定點,但是過程不會很高效。即使對擾動進行測量也于事無補,因為Lambda 整定定律對于負載的行為不做限制,僅僅關心過程而已。
用戶能夠采用的最好的方法就是選擇盡可能小的λ值,以提升控制器的整體響應速度,但是這樣一來控制器的魯棒性就會受到削弱。對于那些要求快速響應的應用場合Lambda整定不是一個好的選擇,因為還有其他更為高效的調(diào)整規(guī)則可以應用于對時間較為敏感的應用場合。
數(shù)學計算上的挑戰(zhàn)
在Lambda整定法的數(shù)學計算方面還有一些深藏的局限性。例如,如果過程本身就是震蕩的,那么Lambda整定就不能用于這一過程。如果開環(huán)沖擊試驗在過程穩(wěn)定之前給過程帶來了抖動,那么這個過程也不能僅僅使用三個參數(shù)Kp、Tp和D就能夠完全描述,那么控制器也不能夠使用Lambda整定定律進行描述,但是還有一些相關的IMC技術可以應對這些情況。
如果死區(qū)時間D非常大,那么數(shù)學計算也有問題。計算中要求得到的Kc和Ti的估計值會隨著D的增加變得越來越不精確。雖然為了提升估計值的精確性已經(jīng)找到了諸多備選方案,但是這些方案也都會帶來一定程度影響。雖然它們看起來完全不一樣,但是卻都能夠獲得幾乎一樣的閉環(huán)性能。一些應用于純PI控制器,一些必須使用在配有微分器的PID控制器上。
對于沒有時間常數(shù)的積分過程來說,Lambda 整定定律的形式會有一些不同。例如液位控制應用中,控制器帶來的沖擊(打開入口閥門)會給過程變量(液位)持續(xù)上升而不會平穩(wěn),這種情況下就存在Lambda整定變種的問題。Lambda整定控制器可以強制積分過程達到穩(wěn)態(tài),但是過程變量達到穩(wěn)定的時間將會更長(可能達到6λ的穩(wěn)定時間),而且在這個過程當中過程變量會過調(diào)。
雖然如此,Lambda整定法還是很簡單、直觀而且防沖擊的整定方法。對于要求使用保守型控制器的應用場合,Lambda整定法將無疑還會繼續(xù)受到歡迎。
沖擊試驗
下面這9步試驗也就是所謂的開環(huán)響應曲線試驗或者步進試驗,它能夠告訴PI控制器所需要知道的關于非震蕩過程的信息,然后PI控制器就能夠藉此對其進行控制:
1.關閉控制器,將其切換至手動模式。
2.等待過程變量達到穩(wěn)態(tài)值。
3.手動“沖擊”或者“步進”過程,強行使控 制作用突然增加B%——過程變量會因此開始 緩慢變化而不是劇烈變化。
4.在趨勢圖上記錄過程變量的反應或者階躍響 應,趨勢圖開始于施加沖擊的時刻(點1), 結束于過程變量再次穩(wěn)定的時刻。
5.在過程變量趨勢線的最陡的位置繪制切線。
6.在過程變量的初始值和結束值處各畫一條水 平線。
7.將這兩條水平線與切線的交叉點標示為點2 和點3.
8.記錄從點1到點2的死區(qū)時間D以及從點2 到點4的過程時間常數(shù)Tp。
9.記錄過程變量從點3到點4的變化,然后除 以B得到過程增益Kp。
Lambda 整定定律
通過過程開環(huán)增益Kp、時間常數(shù)Tp和死區(qū)時間D,可按照如下算式計算出PI控制器的控制效果或控制輸出CO(t):
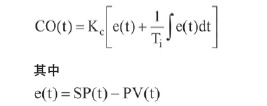
e(t)是過程變量PV(t)和設定點SP(t)之間的差值。
為了使系統(tǒng)閉環(huán)并且無震蕩地在大約4λ的時間內(nèi)穩(wěn)定下來,Lambda 整定定律要求滿足如下兩個條件:
